توابع میانگین نمایی سه گانه

• سيدي فرنوش السادات
• 2024-09-29

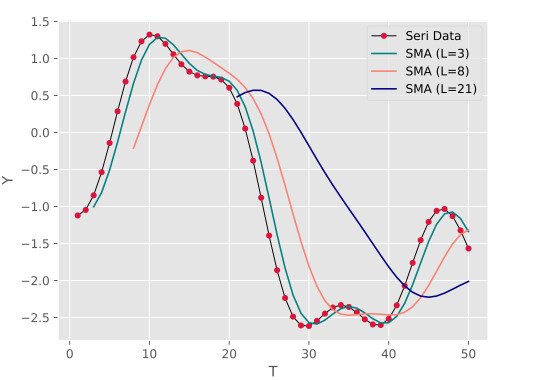
توابع میانگین نمایی سه گانه به عنوان یکی از موضوعات مهم در ریاضیات مدرن شناخته می‌شوند. این توابع در زمینه‌های مختلفی از جمله تحلیل‌های پیچیده و مدل‌سازی‌های ریاضی کاربرد دارند. توانایی مدل‌سازی رفتارهای غیرخطی و تحلیل داده‌های پیچیده از ویژگی‌های برجسته این توابع است.

با توجه به ماهیت خاص این توابع، استفاده از آن‌ها در بسیاری از شاخه‌های علمی، مانند فیزیک، مهندسی و اقتصاد، گسترده است. ویژگی‌های منحصر به فرد آن‌ها باعث می‌شود تا در مسائل پیچیده‌تر، نسبت به دیگر توابع، کاربرد بیشتری داشته باشند.

در این مقاله، به بررسی تعریف، ویژگی‌ها و کاربردهای توابع میانگین نمایی سه گانه خواهیم پرداخت. هدف این است که ضمن معرفی این توابع، نقش آن‌ها را در مسائل علمی و تحقیقاتی مختلف روشن کنیم.

ویژگی‌ها و خصوصیات اصلی این توابع

توابع میانگین نمایی سه گانه دارای ویژگی‌ها و خصوصیات خاصی هستند که آن‌ها را از دیگر توابع متمایز می‌کند. این ویژگی‌ها به طور مستقیم بر کاربردهای مختلف آن‌ها در تحلیل‌های پیچیده و مدل‌سازی‌های ریاضی تاثیر می‌گذارند. برخی از ویژگی‌های برجسته این توابع عبارتند از:

• غیرخطی بودن: این توابع معمولاً رفتار غیرخطی دارند که می‌تواند برای مدل‌سازی پدیده‌های طبیعی و پیچیده مورد استفاده قرار گیرد.
• میزان حساسیت بالا: این توابع به تغییرات جزئی در ورودی‌ها بسیار حساس هستند، که این ویژگی در مسائل دقیق و حساس کاربردی است.
• قابلیت مدل‌سازی فرآیندهای پویا: توابع میانگین نمایی سه گانه می‌توانند فرآیندهای پویا و تغییرات زمانی را به خوبی شبیه‌سازی کنند.
• انعطاف‌پذیری در پارامترها: این توابع امکان تنظیم پارامترهای مختلف را دارند تا متناسب با نیازهای خاص مسائل مختلف، بهینه‌سازی شوند.

این ویژگی‌ها، توابع میانگین نمایی سه گانه را به ابزاری قدرتمند برای تحلیل‌های پیچیده و مدل‌سازی در علوم مختلف تبدیل کرده‌اند. در نتیجه، آن‌ها برای پژوهشگران و متخصصان در بسیاری از حوزه‌ها، از جمله فیزیک و مهندسی، بسیار مفید هستند.

نقش این توابع در ریاضیات مدرن

توابع میانگین نمایی سه گانه در ریاضیات مدرن به عنوان ابزاری کلیدی برای تحلیل‌های پیشرفته شناخته می‌شوند. این توابع به دلیل ویژگی‌های خاص خود، در حل مسائل پیچیده و مدل‌سازی رفتارهای غیرخطی و دینامیکی نقش مهمی ایفا می‌کنند. اهمیت این توابع در کاربردهای مختلف علمی و تحقیقاتی روز به روز بیشتر می‌شود.

مدل‌سازی پدیده‌های طبیعی

یکی از کاربردهای اصلی توابع میانگین نمایی سه گانه در مدل‌سازی پدیده‌های طبیعی است. این توابع توانایی شبیه‌سازی فرآیندهای پیچیده و غیرخطی که در طبیعت رخ می‌دهند، مانند پدیده‌های فیزیکی و شیمیایی را دارند. در بسیاری از مسائل، این توابع می‌توانند به تحلیل دقیق‌تر رفتار سیستم‌ها و پیش‌بینی نتایج کمک کنند.

تحلیل‌های پیچیده و حل معادلات

در بسیاری از شاخه‌های ریاضیات، از توابع میانگین نمایی سه گانه برای حل معادلات پیچیده استفاده می‌شود. این توابع به دلیل انعطاف‌پذیری و ویژگی‌های خاص خود، می‌توانند به حل معادلات دیفرانسیل و مسائل بهینه‌سازی کمک کنند. همچنین در تحلیل داده‌های بزرگ و پیچیده، این توابع می‌توانند برای مدل‌سازی و پیش‌بینی روندها به کار روند.

مقایسه توابع میانگین نمایی با سایر انواع

توابع میانگین نمایی سه گانه در مقایسه با سایر انواع توابع ریاضی ویژگی‌های خاصی دارند که باعث تمایز آن‌ها در کاربردهای مختلف می‌شود. این توابع به دلیل ماهیت خاص خود در مدل‌سازی و تحلیل داده‌ها نسبت به توابع دیگر توانایی‌های منحصر به فردی دارند. مقایسه این توابع با دیگر انواع توابع، به ما کمک می‌کند تا بهتر درک کنیم که چرا و در چه موقعیت‌هایی از این توابع استفاده می‌شود.

مقایسه با توابع نمایی ساده

توابع میانگین نمایی سه گانه از نظر پیچیدگی و دقت نسبت به توابع نمایی ساده تفاوت دارند. در حالی که توابع نمایی ساده تنها با یک عامل نمایی رشد یا کاهش می‌کنند، توابع میانگین نمایی سه گانه می‌توانند رفتار پیچیده‌تری را مدل‌سازی کنند. این توابع برای فرآیندهایی که نیاز به چندین پارامتر و تغییرات متنوع دارند، کاربرد بیشتری دارند.

مقایسه با توابع چندجمله‌ای

توابع چندجمله‌ای معمولاً برای مدل‌سازی فرآیندهایی که به صورت خطی یا تقریباً خطی تغییر می‌کنند مناسب هستند. اما توابع میانگین نمایی سه گانه قادرند به‌طور دقیق‌تر پدیده‌های غیرخطی و پیچیده را شبیه‌سازی کنند. این توابع در مسائلی که نیاز به دقت بالاتر در پیش‌بینی روندها و تغییرات دارند، عملکرد بهتری دارند.